The sequence of real numbers $a_0, a_1,\cdots$ is defined by

\[\begin{aligned} \displaystyle a_0 = -1, \qquad \sum_{k=0}^n \frac{a_{n-k}}{k+1} = 0\text{ for $n\geq 1$.}\end{aligned}\]

Show that $a_n>0$ for all $n\geq 1$.

This was an A2 problem from the 2006 IMO Shortlist. In the footnote of the shortlist it mentioned a complex analysis approach for this problem, but did not say how it’s done. I spent a lot of months before finally finding this solution:

Define $\displaystyle F(x) = \sum_{n\geq 0} a_nx^n$. The given conditions imply $\displaystyle F(x) \cdot \sum_{n \geq 0} \frac{x^n}{n+1} = -1$, but

\[\begin{aligned} \displaystyle \sum_{n\geq 0} \frac{x^n}{n+1} &= \frac{1}{x} \int_{0}^x \sum_{n\geq 0} X^{n}\ dX = -\frac{\ln(1-x)}{x},\\ \therefore F(x) &= \frac{x}{\ln(1-x)}.\end{aligned}\]

We are left to find $\displaystyle a_n= \frac{F^{(n)}(0)}{n!}$. By definition of residue, $\displaystyle \frac{F^{(n)}(0)}{n!} = \text{Res} \left(\frac{F(x)}{x^{n+1}},0\right)$. Let $\displaystyle f(z) = \frac{F(z)}{z^{n+1}} = \frac{1}{z^n \ln(1-z)}$ be a complex function where $\ln$ is the complex logarithm. The arguments are in the range $[-\pi,\pi)$. Therefore the branch cut of $f$ is where $1-z \leq 0 \ (z\in \mathbb{R})$. Apply an anticlockwise keyhole integral around the point $z=1$:

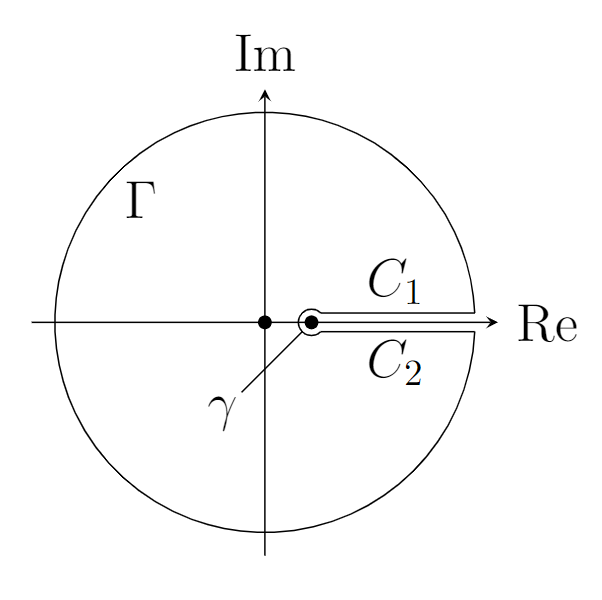
The Contour

\[\begin{aligned} \displaystyle 2\pi i\ a_n= 2\pi i\ \text{Res} \left(\frac{F(x)}{x^{n+1}}\right) = \oint f(z) \ dz =\int_\Gamma + \int_\gamma + \int_{C_1} + \int_{C_2} \end{aligned}\]

Taking the large radius to infinity and the small radius to 0:

\[\begin{aligned} \displaystyle\left|\int_\Gamma \right| = \left| \int_{\varepsilon}^{2\pi-\varepsilon} \frac{Ri\ d\theta}{R^ne^{ni\theta}\ln(1-Re^{i\theta})}\right|\lessapprox \int_{\varepsilon}^{2\pi-\varepsilon} \left|\frac{1}{R^{n-1}\ln(R)}\right|\ d\theta \xrightarrow{R\rightarrow \infty} 0 \end{aligned}\] \[\begin{aligned} \displaystyle \left|\int_\gamma \right| = \left| \int_{\varepsilon}^{2\pi-\varepsilon} \frac{ri\ d\theta}{(1+re^{i\theta})^n\ln(-re^{i\theta})}\right|\lessapprox \int_{\varepsilon}^{2\pi-\varepsilon} \left|\frac{r}{\ln(r)}\right|\ d\theta \xrightarrow{r\rightarrow 0} 0 \end{aligned}\]

For the curve $C_1$,

\[\begin{aligned}\displaystyle \int_{C_1} &= \int_{1+\varepsilon}^R \frac{dx}{(x+i\varepsilon)^n\ln(1-x-i\varepsilon)} \\ &= \int_{1+\varepsilon}^R \frac{dx}{(x+i\varepsilon)^n(\ln|1-x-i\varepsilon|+ i\arg(1-x-i\varepsilon) )} \\ &\rightarrow \int_{1}^\infty \frac{dx}{x^n(\ln(x-1)-i\pi)} \text{ where $\varepsilon \rightarrow 0, R\rightarrow \infty$} \\ &= \int_{1}^\infty \frac{\ln(x-1)+i\pi}{x^n(\ln^2(x-1)+\pi^2)}\ dx\end{aligned}\]

For the curve $C_2$,

\[\begin{aligned}\displaystyle \int_{C_2} &= \int_R^{1+\varepsilon} \frac{dx}{(x-i\varepsilon)^n\ln(1-x+i\varepsilon)} \\&=- \int_{1+\varepsilon}^R \frac{dx}{(x-i\varepsilon)^n(\ln|1-x+i\varepsilon|+ i\arg(1-x+i\varepsilon) )} \\&\rightarrow -\int_{1}^\infty \frac{dx}{x^n(\ln(x-1)+i\pi)} \text{ where $\varepsilon \rightarrow 0, R\rightarrow \infty$} \\&= -\int_{1}^\infty \frac{\ln(x-1)-i\pi}{x^n(\ln^2(x-1)+\pi^2)}\ dx \end{aligned}\]

Combining everything above,

\[\begin{aligned} \displaystyle a_n &= \frac{1}{2\pi i}\int_{1}^\infty \frac{2\pi i}{x^n(\ln^2(x-1)+\pi^2)}\ dx \\&= \int_{1}^\infty \frac{dx}{x^n(\ln^2(x-1)+\pi^2)}>0.\end{aligned}\]